Euler’s Identity Summarized

October 17, 2010November 10, 2010 ~ Sridhar Ramesh ~ 1 Comment

The bullet point version, for busy people:

1) Rings of linear operators: You can do arithmetic with the linear operators on any vector space (functions from the space to itself which turn additions into additions). Addition of such operators is pointwise addition of their output vectors. Multiplication of such operators is composition (performing them in sequence, one after another). Exponentiation is… well:

2) Exponential growth: A function from the domain $[0, \infty)$ to any codomain which turns additions into multiplications describes exponential growth (actually, we can use more general domains as well, but nevermind that for now); such a function can always be thought of as $t \mapsto B^t$ for some nominal base $B$ (which can be identified with $B^1$ , the value of the function at $1$ , but considered as augmented with information specifying how to take fractional powers of this value). The rate of change of this function at the initial input $0$ is, definitionally, the natural logarithm of $B$ , written $\ln(B)$ . Although an exponential map is not generally entirely determined by its output on the input $1$ (because of the need for further information about fractional powers), it is entirely determined by its natural logarithm. Accordingly, general exponentiation can be defined via the equation $\ln(B^p) = p \ln(B)$ , which uniquely determines $B^p$ from $B$ .

3) Rotation: By 1), we can do arithmetic with the rotations upon the vectors of a two-dimensional space. In particular, we can construct the exponential map which sends $t$ to rotation by $t$ many revolutions (in some rotation direction), which, by 2), we may as well give the name $R^t$ . We can then ask about $\ln(R)$ , by which is meant the initial rate of change of this exponential function.

4) The direction of rotation: As a vector rotates, its tangential direction of movement will always be offset from its current direction by a quarter turn; in other words, the ratio of its velocity’s direction to its current direction will always be $R^{1/4}$ .

5) The speed of rotation: As a vector rotates at the speed of one revolution per unit of time, its speed will always be equal to the circumference of the circle it traces, per unit of time; in other words, the ratio of its velocity’s size to its current size will always be $\tau$ per unit of time (where $\tau = 2 \pi$ is the ratio of a circle’s circumference to its radius).

6) The velocity of rotation: Combining 4) and 5), we have complete information about $\ln(R)$ : it consists of rotation by a quarter turn and scaling by a factor of $\tau$ . That is, $\ln(R) = R^{1/4} \tau$ .

7) Notation: Defining $e$ via $\ln(e) = 1$ and recalling the definition of exponentiation from 2), we have that $\ln(e^p) = p \ln(e) = p$ , giving an equivalence between $\ln(B) = p$ and $B = e^p$ . With that equivalence, we can rewrite equation 6) as $R = e^{R^{1/4} \tau}$ . Observing that $R^{1/2} + 1 = 0$ , we can also view $R^{1/2}$ as $-1$ (augmented in a particular canonical way with information about fractional powers), and use the symbol $i$ to denote $(-1)^{1/2} = (R^{1/2})^{1/2} = R^{1/4}$ . Thus we can further rewrite equation 6) into $R = e^{i \tau}$ . Finally, if for some misguided reason we care more about half revolutions than full revolutions, we can take only half the exponential growth of each side, resulting in the rewrite $R^{1/2} = e^{i \pi}$ , which one may write as $-1 = e^{i \pi}$ .

Euler’s Identity, While True, Is Overrated, And Is Also Understood By Small Children

August 3, 2010November 1, 2010 ~ Sridhar Ramesh ~ 8 Comments

For some reason, the view has become standard that the most beautiful equation in all of mathematics is $e^{i \pi} = -1$ . “What a mystical coincidence! What on earth do $e$ , $\pi$ , and $i$ have to do with each other?”* and all that rot. The equation is then often established in a bizarrely roundabout manner with the use of Taylor series, all the more to heighten its appearance as coming out of nowhere and to dull attempts to sully its transcendent beauty with mere understanding. Of course, this involves sweeping under the carpet the forgotten matter of where the Taylor series came from in the first place and whether the proof could be carried out more directly in that original context to begin with.

Bah! Don’t swallow the hype, attractive though it may be. Understanding things is better than finding them amazing. And to understand this equation, to know what it means, is to see that ultimately, all it is claiming is a very simple, intuitively obvious fact: as one rotates a stick, the direction in which the end of the stick is moving is always 90 degrees rotated from the direction in which the stick is pointing. That is, the claim is little more than that the tangent to a circle is perpendicular to its radius.

Sure, it doesn’t look like that’s all it’s saying, but it is. Let’s break it down, using the relevant definitions (if you haven’t yet done so, you should first review how the arithmetic of negative and complex numbers is a way of talking about rotation). First, let’s recall our definitions of $-1$ and $i$ : I’ll use $R$ to mean the action of one full revolution (360 degree rotation). $-1$ , as we saw before, can be thought of as the action of turning halfway through a full revolution (that is, as a 180 degree rotation); in other words, $-1 = R^{1/2}$ . And $i$ is of course defined as the square root of $-1$ ; thus, $i = (-1)^{1/2} = (R^{1/2})^{1/2} = R^{1/4}$ , a quarter revolution (90 degree rotation).

As for $e$ , it is the base of the natural logarithm; that is, $e^x = y$ is by definition equivalent to $x = \ln(y)$ . The natural logarithm, in turn, is defined so that $\ln(x)$ per unit of time is the constant ratio between an exponentially growing quantity’s velocity and the quantity itself, where the quantity multiplies by $x$ over every unit of time. (In calculus jargon, $\ln(x)$ is the derivative of $x^t$ with respect to $t$ when $t = 0$ )

And, at last, the matter of $\pi$ ; first, let’s introduce $r$ for rotation by one radian. Radians, of course, are the normalized unit of rotation in the sense that swinging through one radian is the same as swinging through an arclength equal to the radius; in other words, $\ln(r)$ is $\mathop{\mathrm{sgn}}(\ln(R)) = \frac{\ln(R)}{|\ln(R)|}$ , the purely directional component of $\ln(R)$ with magnitude normalized to $1$ ; i.e., $\ln(r)$ is the direction of the tangent to rotation. Finally, $2 \pi$ is the number of radians in a full revolution; that is, $r^{2 \pi} = R$ , which is to say, $2 \pi = \frac{\ln(R)}{\ln(r)} = |\ln(R)|$ .

Ok, now for the unravelling: the claim $e^{i \pi} = -1$ is, by the definition of $-1$ , just the claim that $e^{i \pi} = R^{1/2}$ . In other words, that $e^{i 2\pi} = R$ (the form the claim would be presented in if one cared more about $2 \pi$ (full revolution) than about $\pi$ (half revolution) [and, indeed, people should…]). By the definition of $e$ , this is just the claim that $i 2 \pi = \ln(R)$ . By the definition of $2 \pi$ , this is just the claim that $i = \ln(r)$ . Finally, by the definitions of $i$ and $r$ , this is just the claim that $R^{1/4}$ is the direction of the tangent to rotation. In other words, this is just the claim that as one rotates a stick, the direction in which the end of the stick is moving is always a quarter revolution (90 degrees) rotated from the direction in which the stick is pointing.

And if you understand that basic geometric fact about rotation, you understand that $e^{i \pi} = -1$ (and that $e^{i \theta} = r^\theta$ in general**). That’s all there is to it.

*: What do $e$ , $\pi$ , and $i$ have to do with each other? Quite a lot! Both $\pi$ and $i$ are all about rotation (remember, $i$ is just a fancy name for 90 degree rotation), and $e$ is all about exponential growth, and rotation is one very simple example of exponential growth (multiplying by the same amount over any equal intervals). So the idea that these are disparate concepts far from having any obvious connections to each other is hogwash; its perpetuation is willful ignorance.

**: Of course, we can always split rotation into its parallel and perpendicular components (which go by the names cosine and sine respectively), and rewrite this as $e^{i \theta} = \cos(\theta) + \sin(\theta) i$ . This is just a change in the presentation of the same simple geometric fact; sometimes it’s helpful to split things into co-ordinates, and sometimes it’s distracting.

[TODO: General cleanup throughout the post, do more hand-holding on explanation of natural logarithm, perhaps more explicitly raise the issue of contexts in which to consider cognate rotations (e.g., 14 degree rotation vs. 374 degree rotation) the same and in which to consider them distinct and how this relates to complex exponentiation and logarithms, including perhaps using color-coding to more explicitly track how the two different perspectives are being used throughout]

(Need a re-summary of the ideas in the above post? Try here)

And… We’re Back!

May 1, 2010May 1, 2010 ~ Alex ~ 2 Comments

Welcome back to the show folks! We shut down for a while there to retool and come up with a new edgier format. For our first show, the theme will be Scandals & Animals…

Seinfeld references aside, we’ll be posting on this blog again, this time with a bit of a change of focus. We’ll be posting on whatever math/philosophy we are interested in, but with much less of an emphasis on approaching things from first principles, and trying to make it accessible to everyone with any interest in math (“Hey look! This math concept is really just this thing you’re familiar with from non-mathematical experience” etc.) Not that there’s anything wrong with that… and not that sort of thing won’t appear necessarily, but we’re feeling more inclined to just do math/philosophy or whatever and not worry about prerequisites. Hopefully this new approach will make it less likely that the blog will become defunct again.

Pop Quiz

October 11, 2009October 11, 2009 ~ Sridhar Ramesh ~ 1 Comment

The Professor loves long, drawn-out, arduous pop quizzes. He can’t get enough of them. But, for him, the fun is all ruined if there’s no surprise; just as much as he loves to spring quizzes on students who haven’t seen them coming, he hates giving quizzes to students who can see them coming.

So the rules of The Professor’s classroom are as follows: every morning, The Professor asks if any students can legitimately prove that they will be given a quiz that day. Any student who cannot is forced to take a six-hour long quiz. Any student who can (with their proof being declared valid by the very expensive, proudly error-free ProofChecker 3000) is sent to recess instead.

No student has ever managed to make it to recess… Oh, they’re all dead-certain each morning that they’ll be given a quiz that day. But any attempt to demonstrate it to the standards of the ProofChecker 3000 always goes the same way: “Professor, the machine rejected my argument as fallacious.” “But of course it did! Why, did you think it would accept your alleged ‘proof’ that you’d be given a quiz today? But then you’d be sent to recess instead of the quiz, clearly demonstrating that ‘proof’ to be invalid. The machine never accepts invalid reasoning; it was very expensive, you know…”

And thus every student gets the quiz every day, and the playground remains perpetually deserted. The quiz is a sure thing.

Yet, trying to show the ProofChecker 3000 the above argument never works. The question is, why not? (Is there something wrong with the argument? What could or would the ProofChecker 3000 point to as its reason for rejecting it?)

[TODO: Expand from here onto Gödel’s (Second) Incompleteness Theorem/Löb’s Theorem]

Sure, Electrical Engineers Use Complex Numbers, But So Do Small Children

June 10, 2009August 10, 2010 ~ Sridhar Ramesh ~ 5 Comments

It’s not uncommon to run across thoughts being voiced along the lines “Imaginary numbers (the square roots of negative numbers) don’t actually exist; at least, not in the same way that real numbers, integers, and so on exist in the world around us. After all, it’s not like you could run sqrt(-5) miles. Imaginary numbers are just a crazy mathematical fantasy which happen, somehow, to give the right results for certain calculations, even though they’re entirely physically meaningless.” That sort of thing, though the exact details vary from case to case. Occasionally, some more sympathetic soul will rejoinder with a reference to the ubiquity of complex numbers in (usually) electrical engineering (of all things!), ostensibly defending imaginary numbers’ legitimacy but, unfortunately, doing so in an unhelpful manner which continues to portray them as weird, arcane concepts of little everyday application.

No doubt, a lot of this stems from the conventional terminology, “Real” and “Imaginary” numbers. Clearly suggestive of the one being genuine in existence while the other must lie somewhere between eccentric fantasy and dangerous delusion… But the names are actually just fossilized ignorance, and, indeed, such thoughts as I opened with above are deeply misguided.

Today, even if you don’t already, you’re going to see why.

Prerequisites for understanding this post: Just about none. In fact, in a way, the less, the better.

Let’s think about sticks. Sticks have lengths. And we can scale these lengths; we can make a stick twice as big, or three times as big, or half as big, or 5.8 times as big, and so on. And it’s in terms of these length ratios that we actually give our measurements; we say “John is 5.8 feet tall” to mean “John is 5.8 times as big as a ruler; i.e., if you scaled a ruler by a factor of 5.8, it’d be as large as John”. And this shows us how to interpret certain numbers as actually about real-world quantities, and life is good. We might even say this shows that 5.8 “exists”, if you want to talk that way, but I’d really rather you didn’t.

And we can interpret addition and multiplication within this framework as well: multiplication means “chain the scalings one after another”: 7 * 5 = 35 because making something 7 times as large, and then making the result 5 times as large has the net effect of making what you started with 35 times as large. Addition means “carry out both scalings, then place the one stick after the other and see where you end up”: 7 + 5 = 12 because something 7 times as large as a ruler laid end to end with something 5 times as large as a ruler ends up at the same place as something 12 times as large as a ruler. So life is really good. We know perfectly well what arithmetic means now.

But wait… we’re missing something. We haven’t accounted for negative numbers. It wouldn’t seem like it means something to scale by a negative factor, so how can we make sense of them? Well, as you are probably familiar, there is a natural convention to adopt. Instead of focusing solely on lengths, we’ll now look at what direction our sticks are pointing in as well; in addition to scaling sticks up or down in size, we’ll also talk about flipping them 180 degrees around to point the other way. So, for example, -1 will mean “Turn your stick 180 degrees”, and -5 will mean “Make your stick 5 times as big and turn it 180 degrees”. But we’ll interpret addition and multiplication exactly the same way as before: -7 * 5 = -35 because “Make it 7 times as large and turn it 180 degrees” followed by “Make it 5 times as large” has the same net effect as “Make it 35 times as large and turn it 180 degrees”. And -7 + 5 = -2 because if I make two copies of my ruler, one 7 times as large but turned around, and the other 5 times as large and unturned, and place the one after the other, the ending point’s location is the same as if I’d just made a copy of my ruler which was twice as large and turned around. So life is super. Looks like negative numbers “exist” as well (but, please, try not to talk that way).

But, hell, once we’ve started talking about turning sticks, why limit ourselves to full half-circle turns? Why not look at quarter-turns, eighth-turns, 23.4 degree turns, and so on?

Why not indeed. Once we toss these in, we get… the complex numbers. All that mysterious i means is “Make a 90 degree turn”. We still interpret addition and multiplication exactly the same way as before; multiplication is still “Do these in sequence” and addition is still “Do these in parallel, lay the results one after another, and see where you end up.” In particular, as far as multiplication goes, since “Turn your stick 90 degrees. Now turn it 90 degrees again.” has the same net effect as “Turn your stick a full 180 degrees”, we see that i * i = -1. That’s it; it’s extraordinarily simple. Life is fantastic. Complex numbers “exist” every bit as much as real numbers; it’s just that the complex numbers express scaling with arbitrary rotation, while real numbers are limited to scaling with half-turn-increment rotation. [And non-negative real numbers express scaling with no rotation at all.]

[You Can’t] Avoid the Noid

May 28, 2009May 28, 2009 ~ Sridhar Ramesh ~ 2 Comments

Prerequisites for understanding this post: Just about none.

Over and over, the following abstract situation tends to pop up: there are things let’s call Xes, and there’s some way to take any finite sequence of Xes and view it as/turn it into an X itself.

For example, we can turn a finite sequence of integers into an integer by adding them up. Or, we can do it a different way, by multiplying them. We can view a finite sequence of textual strings (e.g., <“The”, “quick”, “brown”>) as its concatenation (in this case, “Thequickbrown”), which is itself a textual string. Or a finite sequence of pictures with transparent holes as the composite picture with holes you’d get from laying them on top of each other. And a million other examples; this schema is ubiquitous.

(We could also turn a finite sequence of integers into an integer by just spitting out the length of the sequence, or turn finite sequences of textual strings into the reverse of their concatenation, or other more out there things. These are also instances of the schema as stated above. But they’re not what I’m interested in right now, because… well, wait and see.)

Suppose we were to denote one of these operations by writing out the operands one above another in order. E.g., if we were concerned with addition of integers, we could write

to denote 29. Or, if we were thinking about concatenation of text, we could write

The

quick

brown

to denote Thequickbrown.

All good and well. But now, suppose, instead of adding up the four numbers 3, 12, 4, and 10 at once, I choose instead to first add up 3 and 12 on their own and separately add 4 and 10 on their own, and then add the first of these sums to the second of these sums. How would I notate that?

Well, adding 3 to 12 is denoted by

And adding 4 to 10 is denoted by

And adding the first of these to the second of these is denoted by putting the first above the second, like so

Oh, but wait. This is exactly the same as what we wrote the first time around. First we interpreted it as “The sum of [3, 12, 4, 10]”, but now we’re interpreting it as “The sum of [the sum of [3, 12], the sum of [4, 10]]”. The notation is rather ambiguous.

In fact, it’s even worse than that. Suppose I wanted to take the sum of the empty sequence of integers (i.e., the sequence of length zero). How would I notate it?

Well, like so:

It’s a vertically stacked list that just happens to contain zero integers. And so it denotes their sum (which is 0).

But, if we want to, we can interpret this as all over the place in our original list. For example, there’s one of these empty lists between the 12 and the 4. Or, heck, there’s two. And one at the end! There’s as many or as few as you care to see, wherever you care to see them. So we can interpret our original notation as also meaning “The sum of [3, 12, the sum of [], 4, 10]” or “The sum of [3, 12, the sum of [], the sum of [], 4, 10]”, or “The sum of [the sum of [3], 12, the sum of [], the sum of [], the sum of [4, 10]]” and myriad other bracketings as well.

Highly ambiguous. And thus highly problematic…

Or is it? The sum of [3, 12, 4, 10] = 29. The sum of [the sum of [3, 12], the sum of [4, 10]] = The sum of [15, 14] = 29. The sum of [the sum of [3], 12, the sum of [], the sum of [], the sum of [4, 10]] = The sum of [3, 12, 0, 0, 14] = 29.

Turns out, it doesn’t matter how you read it, it ends up denoting the same thing. So, so far as addition goes, it’s actually coherent to leave out any explicit bracketing. And, as you can see for yourself, this systems works just as well for multiplication of integers, concatenation of textual strings, overlaying of transparencies, and so on. That is, in each of these cases, you can “rebracket” however you like without changing any results, as long as you keep the same terms in the same overall order. Put another way, with such operations, it’s perfectly coherent to act as though there were never any need to consider bracketing in the first place. Such an operation is called a monoid.

But, watch out: it doesn’t always work out as well (i.e., not every operation that turns sequences of Xes into Xes is a monoid). E.g., with concatenate-and-reverse

Dog

Cat

Fox

is equal to xoFtaCgoD if we think of it as concatenate-and-reverse [Dog, Cat, Fox], but it is equal to xofDogCat if we think of it as concatenate-and-reverse [concatenate-and-reverse [Dog, Cat], Fox]. Hell, even worse, if we just wrote

Dog

then we could think of this as either meaning straight-up Dog or as meaning concatenate-and-reverse [Dog] = goD. So with concatenate-and-reverse, we can’t get away with avoiding explicit brackets, as it is very much not invariant under rebracketing; i.e., it is not a monoid.

But, no matter; incredibly many things are. So now let’s return to the first paragraph with some refinement:

Over and over, the following abstract situation tends to pop up: there are things let’s call Xes, and there’s some way to take any finite sequence of Xes and view it as/turn it into an X itself, in a manner which doesn’t demand explicit bracketing. Such an operation is called a monoid. And since mathematics (/logic/mathematical logic…) is all about studying common abstract patterns, we’ll be talking quite a bit more here about properties of monoids, different ways to think about monoids, specific examples of monoids, applications of the theory of monoids, generalizations of monoids (and properties of, different ways to…, for these generalizations) and so on in the posts to come.

Ultrafilters and Ultraproducts – Part 1

May 7, 2009May 8, 2009 ~ Alex ~ Leave a comment

Suppose I asked you to name a subset of the natural numbers that contained ‘most’ of them.

You might reply “‘Most’ could mean a lot of things”, or “Why are you trying to apply this sort of vague term to something so concrete as the natural numbers? Don’t you know what happens when you do things like that? Paradox, my friend.” So, maybe you think infinite sets are concrete, maybe you think you’re my friend, and maybe you think that every natural number being both ‘large’ and ‘small’ is a problem.

(If there’s no smallest large number, then they’re all large, even 0, but if there’s a smallest, say k, then k-1 is smaller and still large, a contradiction. So, either there’s a smallest large number – for example, 1,090,037 is large, but 1,090,036 is not – or else all numbers are large… or this is just a silly game to play.)

But suppose you ignore those things, and decide to play along with me, just for fun. Being forced to play my game you might start off, coyly, by proposing 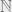$\mathbb{N}$ itself. A good choice actually – I would definitely agree that that set contains most of the natural numbers. How about the emptyset, 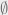$\emptyset$ , the set containing no numbers, I ask. No, of course that’s not ‘most’, you’d say (I hope!). So we’ve got somewhere to start then: everything is most of something, and nothing is not most of anything.

Perhaps your next proposal might be along the following lines: if we take the natural numbers and remove a finite number of them, say the set $\{n < 12\}$ , then we are left with a set that counts as ‘most’ of the naturals: $\{n \geq 12\}$ . Happily, I’d agree – even if we take arbitrarily large finite amounts of elements out of the set, there are still infinitely many left, and an infinite set is certainly much larger than a finite set.

Okay, what else? I’ll answer for you: if some set of natural numbers counts as ‘most’ of them, then I’m sure you’d agree that adding one more number (or many more) to the set leaves us with another set containing most natural numbers. Now here’s the tricky one – suppose I’ve got two sets of naturals, and we agree that teach contains ‘most’ of 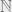$\mathbb{N}$ ; let’s call these sets A and B. As an example, we could let A be $\{n > 12\}$ and B be $\{1, 5, 21\} \cup \{n > 100\}$ . (Both sets miss only finitely many numbers, so by your earlier idea, they’re both ‘most’). Now form a new set, the intersection of A and B, by taking one of them, and removing any number not in both sets. We’d be left with $A \cap B = \{21\} \cup \{n > 100\}$ , a set that still conforms to our earlier rule, and which should still count as ‘most’.

Okay, then we’ve recovered a definition. Given a set X, a filter on X, call it $\mathcal{F}$ , is a notion of what subsets count as ‘most of X’; that is, it is a collection of ‘large’ subsets of X following the following rules:

(i) $X \in \mathcal{F}, \emptyset \notin \mathcal{F}$

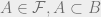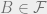
(ii) if $A \in \mathcal{F}, A \subset B$ , then $B \in \mathcal{F}$

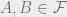(iii) if $A, B \in \mathcal{F}$ then $A \cap B \in \mathcal{F}$

First thing to notice is that even with a fixed X, there are many possible filters on it – just as two reasonable people might disagree on what counts as ‘most’ of something, there exist many different notions of ‘most’ on any given set. For example, on 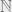$\mathbb{N}$ , we might ask whether the set of even numbers is large. What about the odds? Neither? Both? There are filters for each of these options except the last. Why not the last? Well, the thing to notice is that the evens are the complement of the odds – there is no number they have in common. Thus, their intersection is empty – so if a filter contains one, and the other – and so, they both contain ‘most’ naturals – then their intersection, by (iii), must also be in the filter. But (i) prohibits this. This is true of any set A – if it is in the filter, then its complement is not, and vice versa (and the other option is that neither is in).

Now, there are also going to be some filters which we will want to discount, even though they are not excluded in advance. These are filters that contain a finite subset (i.e. say that a finite set is ‘most’ of X). Intuitively, finite sets shouldn’t be large. If a finite set counts as ‘most’, then its complement, an infinite set missing only finitely many elements, would not count as large, as I just mentioned above. The rules above don’t exclude these filters, and we’ll have a convenient way to get rid of these when we shift our attention to ultrafilters, so I wont bother explicitly excluding them.

Before moving on to an ultrafilter, I think we need a reason to live – or at least, a reason to care about filters and ultrafilters. So, lets consider the following progression: 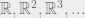$\mathbb{R}, \mathbb{R}^2, \mathbb{R}^3,...$ . What should come at the end of this sequence?

Let’s call it $\mathbb{R}^\infty$ . $\mathbb{R}^n$ is the set of n-tuples of reals, so $\mathbb{R}^\infty$ is the set of infinite sequences of reals indexed by 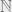$\mathbb{N}$ (so maybe we should have called it $\mathbb{R}^\omega$ ). The objects in this set are just sequences of reals which we came to know and love in calculus class. You did, right? Recall from calculus class that sequences either converge or don’t converge. If they converge, they converge to some real number, and if they don’t, there’s two reasons why that might happen. 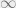First, they might go to $\infty$ or $-\infty$ , and secondly, they might diverge because they just don’t any particular tendency as the sequence progresses – for example, the sequence $(0,1,0,1,...)$ . 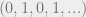So we can say that every sequence has a limit in $\mathbb{R}\cup\{\pm\infty\}$ or else has no limit.

Why does this matter? Well, because, if we play our cards right, we can get ourselves a nice ordering on $\mathbb{R}^\infty$ (or something like it) that turns it into a nice extension of the real numbers. And one which contains infinitesimal and infinite elements in a perfectly consistent, understandable and useful fashion. I’ll leave explaining why such an extension would be a nice thing to have for a later post. But for now, it basically gives us a sandbox other than the real numbers in which we can do all the usual things in calculus (differentiate, integrate, make theorems etc.) but without epsilson-delta arguments, and with what some would argue is a higher degree of intuitiveness. (Sridhar may want to discuss an alternate construction of infinitesimal calculus, but this will remain, deaf to what he has to say, my favourite.)

Now, why aren’t any of the existing orderings on $\mathbb{R}^\infty$ good enough for us? Here’s one reason: the following sequences all have 1 as their limit

$(a_n) = (1,1,1,...),(b_n) = (2,1,1,1,...), (c_n) = (1,2,1,1,1,...)$

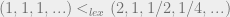however, they are all different sequences so they are all different elements of $\mathbb{R}^\infty$ . And so, they need to be put in some order. Which should be ‘greater’ than which? Well, if we put them in lexicographic ordering, we get $(b_n) > (c_n) > (a_n)$ and if we reverse the lexiographic ordering we get the reverse, and neither is particularly appealing. Similarly, $(1,1,1,...) <_{lex} (2,1,1/2,1/4,...)$ , even though the first has limit 1 and the second has limit 0.

Ultrafilters let us deal with this problem gracefully – we will capture the limit rule that changing a finite number of entries in a sequence doesn’t change the limit by saying that the sequences 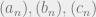$(a_n),(b_n),(c_n)$ are all equal! How does this work? What we do, in effect, is say that two sequences are in some relation (<, >, or =) to each other just if most of their indices have that property. 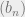That is, one sequence $(a_n)$ will be less than another, $(b_n)$ , just if on a large set of indices i, we have $a_i < b_i$ .

Okay, so why the ultra? Well, suppose we have a filter on the natural numbers that says that neither the even numbers nor the odds are large. And consider the sequences $(a_n) = (0,1,0,1,...)$ and $(b_n) = (1,0,1,0,...)$ – in order to figure out which of these sequences is greater than the other (or if they are equal), we check if they have that property on a large set. However, since neither the evens nor the odds are large, there is no large set where the differ (so neither is greater than the other), and since they are equal nowhere, there is no large set where they are equal. Thus, our filter’s indecision about the evens and odds has become an indecision about which sequence is greater than which.

To solve this, we add the following restriction to the definition of a filter to get an ultrafilter:

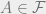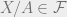(iv) for every subset A of X, either $A \in \mathcal{F}$ or $X/A \in \mathcal{F}$ .

That is, every set is either large, or its complement is large. Now, you may smell arbitrariness coming your way. And the above example is also an example of this: to get an ultrafilter, we need to make some decision, arbitrary though it may be, about whether the evens or odds are large. As well, there will be many other subsets and their complements about which a filter is not required to make a decision. Thus, in order to make ultrafilters, there is going to be an infinite amount of arbitrary decision making going on. I’ll stop here, and continue in the next post with ultrafilters, and more of the story of $\mathbb{R}^\infty$ .

Arrow’s Impossibility Theorem and Ultrafilters

April 19, 2009August 10, 2010 ~ Sridhar Ramesh ~ 6 Comments

Let’s kick this blog off with a post about Arrow’s Impossibility Theorem. The content of this theorem is actually extremely closely related to ultrafilters, and, in fact, the eponymous “impossibility” is essentially the same as a very basic fact about ultrafilters on finite sets. Yet, for some reason, I have rarely (if ever) seen the theorem presented in such a way as even mentions this connection (e.g., the word “filter” appears not once in the relevant Wikipedia article, nor in any of the references within it). A shame, which I shall rectify in this post.

[This post is still a bit unpolished and should be made more readable; however, I decided to publish it first and then come back and improve it, rather than letting the blog stagnate idly. This may become the general modus operandi for Pleasant Feeling]

Current requirements to understand this post: Basic knowledge of what filters and ultrafilters are [I shall probably come back and expand this post to actually kick off an introduction to the concepts for those who don’t already know]

Suppose you have a fixed set of voters and a set of ballot options (aka, candidates) for them to choose between. By a (deterministic) voting system on these voters and ballot options, we mean some function which takes as input any assignment from voters to their preferences (expressed as a linear ordering upon the ballot options) and produces as output some cumulative ranking of the ballot options (again, expressed as a linear ordering upon the ballot options). What Arrow’s Impossibility Theorem shows is that, if there are at least 3 ballot options, the voting systems satisfying some basic desirable criteria come only in one very particular (in some cases, rather undesirable) form.

What criteria exactly? Well, the first is “Pareto efficiency”, aka “unanimity”: if all voters have the exact same preferences, then the cumulative ranking should be the same as this. Surely, this is the most natural, basic voting system property one could ask for.

The second criterion is “independence of irrelevant alternatives” (IIA): in the cumulative ranking, the relative position of any two ballot options depends only on the voters’ relative preferences between them (i.e., to figure out if option A beats option B in the cumulative ranking, one only needs to ask which voters ranked A higher than B and which ranked B higher than A; one doesn’t need to know anything about how voters felt about any other, “irrelevant” options). This is one way of formalizing that there should be no “spoiler” effect (Nader shouldn’t be able to steal votes away from Gore to win the election for Bush).

Let’s start exploring the effects of these criteria on the design of a voting system. First, for simplicity’s sake, we’ll act as though there are exactly 3 ballot options (we’ll use A, B, and C to denote arbitrary ballot options, with different letters being distinct options), and we’ll restrict voters to turning in preferences without ties, but we’ll not explicitly restrict the cumulative ranking from having ties. All of these assumptions could be dropped/changed, but as they only make things easier for the voting system designer, our impossibility results will immediately generalize even to these other cases.

Ok, so what can we conclude from these criteria? Well, by independence of irrelevant alternatives, we know that whether A beats B in the final ranking or not just depends on which set of voters choose A over B [and which set chooses the opposite, but as voters’ preferences have no ties, these two sets are complements and so the latter is redundant data on top of the former]; so, we’ll say that a set of voters M wins for A over B if the cumulative ranking has A beating B when the voters who prefer A to B are precisely those in M. The Pareto efficiency condition then becomes just that the set of all voters wins for every candidate over every other candidate. The voting system is entirely determined by this ternary relation, so let’s see what kind of properties it has.

Suppose M wins for A over B. Then consider the situation where voters vote as follows:

In M: A > B > C
Outside M: B > C > A

Since the voters who choose A over B are precisely those in M, A will beat B. Furthermore, since everyone chooses B over C, B will beat C; thus, transitively, A will beat C. Since the voters who chose A over C are precisely those in M, we see that M wins for A over C as well.

So we’ve proven that if M wins for A over one candidate, then it also wins for A over any other candidate; thus, we can speak just of “winning set for A over others” rather than “winning set for A over B” and such.

But, everything here is symmetric; just reversing all the orders above, we see that if a set wins for some other candidate over A, then it wins for any candidate over A, and so we can speak generally of “winning set for others over A”. [And, of course, instead of A in these, we could use any other candidate]

And so we have that winning set for A over others = winning set for A over B = winning set for others over B = winning set for C over B = winning set for C over others. Thus, any two candidates have the same winning sets over others, and so we can just speak of winning sets in absolute terms, without having to specify which candidates are involved. Now we just have to see what kind of properties the system of winning sets is constrained to have.

By the unanimity condition, the set of all voters is a winning set. Furthermore, suppose M and N are winning sets and consider the situation where voters vote as follows:

In M and N: A > B > C
In M but not N: C > A > B
In N but not M: B > C > A
In neither M nor N: C > B > A

In this case, the voters who choose A over B are precisely the ones in M, and the voters who choose B over C are precisely the ones in N; thus, the result must be that A wins over B and B wins over C. But this means that A wins over C; since the voters who choose A over C are precisely the ones in both M and N, we see that the intersection of M and N must win for A over C. So, the winning sets are closed under intersection as well.

Now, let us demonstrate that the winning sets are upwards closed. Suppose M is a winning set, N is a superset of M, and voters vote as follows:

In M: A > B > C
In N but not M: B > A > C
Outside N: B > C > A

Then the voters who choose A over B are those from M, so A beats B. And everyone chooses B over C, so B beats C. Thus, transitively, A beats C; as the voters who choose A over C are precisely those in N, we have that N is a winning set as well.

So we see that winning sets are closed under finite intersection and upwards closed, which makes them a filter. Finally, let’s show that they actually form an ultrafilter: this means of every set of voters, either it or its complement wins, but not both. The not both part is automatic (two candidates can’t both beat each other), and the first part is nearly as automatic; we just have to show that there can’t be any ties. Well, suppose there existed some tying set M (i.e., such that neither M nor its complement were winning sets). Then consider the voting situation

In M: A > B > C
Outside M: B > C > A

In this case, A ties with B and A ties with C, so transitively, we should have that B ties with C. However, by unanimity, we also have that B beats C, which is a contradiction. Thus, we can conclude, there cannot actually exist any tying sets; no one ever actually ties.

Thus, the winning sets necessarily form an ultrafilter. Conversely, it is readily seen that any ultrafilter gives a suitable system of winning sets (you can verify this directly, but those in the know should recognize this as just an instance of Łoś‘s Theorem, the voting system being naught but an ultraproduct). And so we have that (with at least 3 candidates), the Pareto efficient voting systems satisfying IIA are precisely those given by ultrafilters. This is Arrow’s Impossibility Theorem (albeit phrased in a more general form than than it is usually given in).

Why “Impossibility”, you ask? Well, in particular, the ultrafilters on finite sets are precisely the principal ones; thus, on a finite set of voters, the only Pareto efficient IIA voting systems are “dictatorships”; there is a fixed voter whose preferences are always taken verbatim as the overall result. Which is to say, on a finite set of voters, it is impossible to construct a voting system satisfying the above criteria as well as that of non-dictatorship (this, of course, being the way AIT is usually stated).

	Arrow’s Imposs… on Arrow’s Impossibility Th…
	Ultrafilters, Ultrap… on Arrow’s Impossibility Th…
	Reshma Bhatnagar on Sure, Electrical Engineers Use…